Energetic and structural analysis of a database of PtAu nanoclusters

In this tutorial we are going to go beyond the core functionality of TurboGAP and focus instead of the analysis and interpretation of the results that can be obtained with TurboGAP. We will look at the energetics and structural characteristics of small PtAu alloy nanoparticles (NPs). Note: at the time of writing this tutorial the PtAu GAP used to generate the NPs is not publicly available. For this reason you will need to skip the step on NP generation, but can still download the pregenerated database so that you can run the rest of the tutorial.

Tutorial difficulty: HARD

Prerequisites for this tutorial

• A TurboGAP installation, only for the NP database generation step, which you can skip by downloading the database;
• An ASE installation;
• Numpy;
• A plotting program. I will use gnuplot and provide the corresponding code, but it can be replaced by something else;
• An ase_tools installation;
• A quippy installation (Python interface for the QUIP code);
• A program for ball-and-stick visualization of atomistic structures. I will use the Python version of Ovito.

Generating the nanoparticles

WARNING1: the options below are just enough to generate example NPs for this tutorial. The annealing and quenching times are most definitely too short to generate stable "publication-quality" NPs.

WARNING2: to be able to generate the nanoparticles with TurboGAP, you'll need to download the gap_files from Zenodo. If you want to skip this step (e.g., to speed up the process of going through the tutorial), you can still try to follow the scripts and simulation logic, and download the database of relaxed NPs from the next section.

We are going to generate a database of PtAu NPs with variable size and composition. In particular, we will generate 10 NPs per size and composition, where the Pt and Au contents will be varied at 10% increments and the size will be varied at 5 atoms increments from 25 to 50. This will lead to 660 unique PtAu NPs (including pure Pt and Au NPs). The first step is to generate a set of random initial structures with the desired properties. The following Python code will take care of generating random distributions of atoms with roughly spherical shapes where the interatomic distances are not too small to avoid highly energetic starting configurations that may be prone to "blowing up". Make sure to create the init_xyz directory before proceeding.

 1 import numpy as np
 2 from ase.io import write
 3 from ase import Atoms
 4 
 5 a = 3.9668
 6 d_min = 2.
 7 
 8 append = False
 9 num = 1
10 
11 nrand = 10
12 for n in range(25,50+1,5):
13     for f_Au in np.arange(0.,1.+1.e-10,0.1):
14         for i in range(0, nrand):
15             R = (a**3 / 4. * n * 3./4./np.pi)**(1./3.)
16 
17             pos = []
18             while len(pos) < n:
19                 this_pos = (2.*np.random.sample([3]) -1) * R
20                 d = np.dot(this_pos, this_pos)**0.5
21                 if d > R:
22                     continue
23                 if len(pos) == 0:
24                     pos.append(this_pos)
25                 else:
26                     too_close = False
27                     for other_pos in pos:
28                         dv = this_pos - other_pos
29                         d = np.dot(dv, dv)**0.5
30                         if d < d_min:
31                             too_close = True
32                             break
33                     if not too_close:
34                         pos.append(this_pos)
35 
36             n_Au = int(n*f_Au)
37             n_Pt = n - n_Au
38 
39             atoms = Atoms("Pt%iAu%i" % (n_Pt, n_Au), positions = pos, pbc=True)
40             write("init_xyz/all.xyz", atoms, append = append)
41             atoms.center(vacuum = 10.)
42             write("init_xyz/%i.xyz" % num, atoms)
43             num += 1
44             append = True

The resulting structures will look something like this:

Next, we will run some TurboGAP workflows consisting of high-temperature annealing, where the annealing temperature (1150 K) is the optimal temperature for Pt (as found in Ref.), and the PtAu and Au temperatures are estimated from that one scaling by the ratio of experimental melting temperatures of pure Au and Pt (and interpolating linearly). All temperatures are further scaled by a global parameter (f = 1.1 below; you can try changing this number to check if it improves the structures). High-[math]\displaystyle{ T }[/math] annealing is followed by a rapid quench down to 100 K, and this is again followed by gradient descent static relaxation. The whole workflow can be reproduced with the following Bash script.

  1 # This value scales the annealing temperature
  2 f=1.1
  3 
  4 mkdir -p trajs/
  5 mkdir -p logs/
  6 mkdir -p trajs/trajs_$f
  7 mkdir -p logs/logs_$f
  8 
  9 for i in $(seq 1 1 660); do
 10 
 11 SECONDS=0
 12 
 13 n_Au=$(awk '{if($1=="Au"){n+=1} else {n+=0}} END {print n}' init_xyz/$i.xyz)
 14 n_Pt=$(awk '{if($1=="Pt"){n+=1} else {n+=0}} END {print n}' init_xyz/$i.xyz)
 15 
 16 T=$(echo $n_Au $n_Pt | awk -v f=$f '{print f*($1/($1+$2)*750.+$2/($1+$2)*1150.)}')
 17 
 18 echo "Doing $i/660..."
 19 
 20 ##########################################
 21 # Anneal at $T for 1 ps
 22 cat>input<<eof
 23 atoms_file = 'init_xyz/$i.xyz'
 24 pot_file = 'gap_files/PtAuH.gap'
 25 
 26 n_species = 3
 27 species = Pt Au H
 28 
 29 md_nsteps = 250
 30 md_step = 4.
 31 
 32 optimize = "vv"
 33 thermostat = "bussi"
 34 t_beg = $T
 35 t_end = $T
 36 tau_t = 10.
 37 eof
 38 
 39 mpirun -np 4 turbogap md &> /dev/null
 40 n=$(head -1 trajectory_out.xyz | awk '{print $1+2}')
 41 tail -$n trajectory_out.xyz > atoms.xyz
 42 mv thermo.log logs/logs_$f/anneal_$i.log
 43 ##########################################
 44 
 45 
 46 
 47 ##########################################
 48 # Quench to 100K over 1 ps
 49 cat>input<<eof
 50 atoms_file = 'atoms.xyz'
 51 pot_file = 'gap_files/PtAuH.gap'
 52 
 53 n_species = 3
 54 species = Pt Au H
 55 
 56 md_nsteps = 250
 57 md_step = 4.
 58 
 59 optimize = "vv"
 60 thermostat = "bussi"
 61 t_beg = $T
 62 t_end = 100.
 63 tau_t = 100.
 64 
 65 write_xyz = 250
 66 eof
 67 
 68 mpirun -np 4 turbogap md &> /dev/null
 69 n=$(head -1 trajectory_out.xyz | awk '{print $1+2}')
 70 tail -$n trajectory_out.xyz > atoms.xyz
 71 mv trajectory_out.xyz trajs/trajs_$f/$i.xyz
 72 mv thermo.log logs/logs_$f/quench_$i.log
 73 ##########################################
 74 
 75 
 76 
 77 ##########################################
 78 # Relax
 79 cat>input<<eof
 80 atoms_file = 'atoms.xyz'
 81 pot_file = 'gap_files/PtAuH.gap'
 82 
 83 n_species = 3
 84 species = Pt Au H
 85 
 86 md_nsteps = 1000
 87 
 88 optimize = "gd"
 89 eof
 90 
 91 mpirun -np 4 turbogap md &> /dev/null
 92 n=$(head -1 trajectory_out.xyz | awk '{print $1+2}')
 93 tail -$n trajectory_out.xyz >> trajs/trajs_$f/$i.xyz
 94 mv thermo.log logs/logs_$f/relax_$i.log
 95 rm trajectory_out.xyz
 96 rm input
 97 ##########################################
 98 
 99 
100 echo "    ... in $SECONDS s"
101 
102 done

The trajectory files with exactly three snapshots (system after annealing, quench and relaxation) will be save into the trajs/traj_1.1 directory. As mentioned at the top of this section, the chosen parameters are way too lax to make properly relaxed NPs.

Construct the convex hull of NP stability

We are now going to collect all the 660 relaxed structures and put them into an ASE "database" XYZ file: this is simply a file with .xyz extension with all the individual XYZ files (containing only the final snapshot) concatenated. The following Python script will collect the data:

1 from ase.io import read,write
2 
3 # Read in the database
4 db = []
5 for i in range(1,660+1):
6     atoms = read("trajs/trajs_1.1/%i.xyz" % i, index=-1)
7     db.append(atoms)
8 
9 write("db0.xyz", db)

While we upload the PtAu GAP to a public repository (needed to run the workflow above), you can download a sample db0.xyz file here.

Now, let's plot the convex hulls for the different NP sizes. First, create a directory called hulls, to keep the top directory a bit cleaner, and run the following code.

 1 from ase.io import read
 2 import numpy as np
 3 
 4 db = read("../db0.xyz", index=":")
 5 
 6 all = {}
 7 Ns = []
 8 xs = {}
 9 
10 for atoms in db:
11     N = len(atoms)
12     x = np.round(atoms.symbols.count("Pt")/N, decimals = 8)
13     if (N,x) not in all:
14         all[N,x] = [atoms.info["energy"]/N]
15     else:
16         all[N,x].append(atoms.info["energy"]/N)
17     if N not in Ns:
18         Ns.append(N)
19     if N not in xs:
20         xs[N] = [x]
21     elif x not in xs[N]:
22         xs[N].append(x)
23 
24 for N in Ns:
25     x_vals = []
26     e_vals = []
27     for x in xs[N]:
28         for e in all[N,x]:
29             if x not in x_vals:
30                 x_vals.append(x)
31                 e_vals.append(e)
32             else:
33                 for i in range(0, len(x_vals)):
34                     if x == x_vals[i] and e < e_vals[i]:
35                         e_vals[i] = e
36     if 0. in x_vals and 1. in x_vals:
37         i0 = np.where([x == 0. for x in x_vals])[0][0]
38         i1 = np.where([x == 1. for x in x_vals])[0][0]
39         e0 = e_vals[i0]
40         e1 = e_vals[i1]
41         idx = np.argsort(x_vals)
42         x_vals = np.array(x_vals)[idx]
43         e_vals = np.array(e_vals)[idx]
44         for i in range(0, len(x_vals)):
45             x = x_vals[i]
46             e_vals[i] -= e1*x + e0*(1.-x)
47         f = open("%i.dat" % N, "w")
48         for i in range(0, len(x_vals)):
49             if i == 0 or i == len(x_vals) or e_vals[i] <= 0.:
50                 print(x_vals[i], e_vals[i], file=f)
51         print("", file=f)
52         print("", file=f)
53         for x in xs[N]:
54             for e in all[N,x]:
55                 print(x, e-e1*x-e0*(1.-x), file=f)
56         f.close()

After extracting and collecting the NP energies in a suitable format, you can easily plot the results. This is a sample gnuplot code that can do the job.

 1 set term pngcairo size 1200,480
 2 
 3 set output "hulls.png"
 4 
 5 set multiplot layout 1,6
 6 
 7 set xlabel "x in Pt_{x}Au_{1-x}"
 8 set ylabel "Energy above hull (eV/atom)"
 9 
10 set yrange [-0.02:0.12]
11 set xtics 0.5
12 set mxtics 1
13 
14 do for [i=25:50:5] {
15 set title "N = ".i
16 plot "".i.".dat" index 1 pt 7 not, "" index 0 pt 6 ps 1.2 lw 4 w lp not
17 }

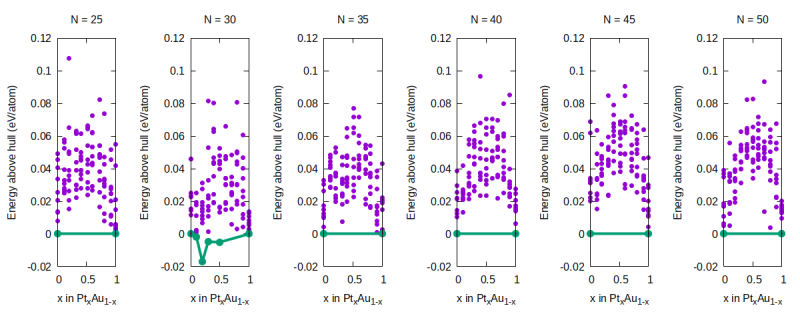
In the figure below you can see how most of the alloy data (purple dots at [math]\displaystyle{ x \neq 0,1 }[/math]) are higher in energy than the linearly interpolated values for the pure NP of the same size. The only exception are the NPs for [math]\displaystyle{ N = 30 }[/math]. If the simulations had been carried out carefully, this would mean that alloying is energetically unfavorable since, for a given composition, a mixture of pure NPs is lower in energy than the alloyed NPs with the same average composition. In reality, 1) our annealing time was way too short to properly sample low minima of the alloy potential energy surface and 2) we are omitting the configurational entropy of the alloy which lowers its free energy of formation at finite temperature (we are only looking at the potential energy).

Analyze the structure

To grasp the overall structural features of our NPs, we are going to global similarity kernels based on SOAP descriptors, as described in Ref. and Ref.. First, we use Quippy to compute the SOAP descriptors (using the soap_turbo implementation) of our NPs. With these descriptors, which are a set of vectors (one per atom) for each NP, [math]\displaystyle{ \{ \textbf{q}_i \} }[/math], we construct the kernels. These kernels constitute a measure of similarity between individual atomic environments, and are given as dot products, [math]\displaystyle{ k(i,j) = (\textbf{q}_i \cdot \textbf{q}_j)^\zeta }[/math], where [math]\displaystyle{ k(i,j) \in [0,1] }[/math] (0 means nothing alike and 1 identical up to symmetry operations). With these individual kernels we compute the global kernels, which allow us to compare whole NPs, [math]\displaystyle{ K(I,J) = (\sum_{i \in I} \sum_{j \in J} k(i,j)) / \sqrt{K(I,I) K(J,J)} }[/math]. From the kernels, we construct a distance metric, [math]\displaystyle{ d(I,J) = \sqrt{1-K(I,J)} }[/math]. FInally, we use this distance to build a dissimilarity matrix which is passed to the cl-MDS code, which performs k-medoids clustering and hierarchical MDS-based embedding of the data points.

 1 from ase import cluster
 2 from quippy.descriptors import Descriptor
 3 from quippy.convert import ase_to_quip
 4 import numpy as np
 5 from ase.io import read,write
 6 import cluster_mds as clmds
 7 import kmedoids
 8 
 9 
10 db = read("db0.xyz", index=":")
11 
12 ###############################################################################################
13 # This builds the global kernel for the NP-wise cl-MDS map
14 n_cl = 22 # number of clusters
15 cutoff = 5.7; dc = 0.5; sigma = 0.5
16 zeta = 6
17 soap = {"Au": 'soap_turbo alpha_max={8 8} l_max=8 rcut_soft=%.4f rcut_hard=%.4f \
18                atom_sigma_r={%.4f %.4f} atom_sigma_t={%.4f %.4f} \
19                atom_sigma_r_scaling={0. 0.} atom_sigma_t_scaling={0. 0.} \
20                radial_enhancement=1 amplitude_scaling={1. 1.} \
21                basis="poly3gauss" scaling_mode="polynomial" species_Z={78 79} \
22                n_species=2 central_index=2 central_weight={1. 1.} \
23                compress_mode=trivial' % (cutoff-dc, cutoff, *(4*[sigma])),
24         "Pt": 'soap_turbo alpha_max={8 8} l_max=8 rcut_soft=%.4f rcut_hard=%.4f \
25                atom_sigma_r={%.4f %.4f} atom_sigma_t={%.4f %.4f} \
26                atom_sigma_r_scaling={0. 0.} atom_sigma_t_scaling={0. 0.} \
27                radial_enhancement=1 amplitude_scaling={1. 1.} \
28                basis="poly3gauss" scaling_mode="polynomial" species_Z={78 79} \
29                n_species=2 central_index=1 central_weight={1. 1.} \
30                compress_mode=trivial' % (cutoff-dc, cutoff, *(4*[sigma]))}
31 
32 d1 = Descriptor(soap["Pt"])
33 d2 = Descriptor(soap["Au"])
34 
35 qs = []
36 for atoms in db:
37     at = ase_to_quip(atoms)
38     q1 = d1.calc_descriptor(at)
39     q2 = d2.calc_descriptor(at)
40     if q1.shape == (1,0):
41         q = q2
42     elif q2.shape == (1,0):
43         q = q1
44     else:
45         q = np.concatenate((q1, q2))
46     qs.append(q)
47 
48 kern = np.zeros([len(qs), len(qs)])
49 for i in range(0,len(qs)):
50     for j in range(i,len(qs)):
51         k = 0.
52         for i2 in range(0, len(qs[i])):
53             for j2 in range(0, len(qs[j])):
54                 k += np.dot(qs[i][i2], qs[j][j2])**zeta
55         kern[i,j] = k
56         kern[j,i] = k
57 
58 kern_n = np.zeros([len(qs), len(qs)])
59 for i in range(0,len(qs)):
60     for j in range(0,len(qs)):
61         kern_n[i,j] = kern[i,j] / np.sqrt(kern[i,i] * kern[j,j])
62 
63 dist = np.zeros([len(qs),len(qs)])
64 for i in range(0,len(qs)):
65     dist[i, i] = 0.
66     for j in range(i+1,len(qs)):
67         dist[i, j] = np.sqrt(1.-kern_n[i,j])
68         dist[j, i] = np.sqrt(1.-kern_n[i,j])
69 
70 M, C = kmedoids.kMedoids(dist, n_cl, n_iso=n_cl//2, init_Ms="isolated", n_inits=10)
71 data = clmds.clMDS(dist_matrix = dist)
72 data.cluster_MDS([n_cl,1], weight_cluster_mds=2., weight_anchor_mds=10., init_medoids=M)
73 list_sparse = data.sparse_list
74 XY_sparse = data.sparse_coordinates
75 C_sparse = data.sparse_cluster_indices
76 M_sparse = data.sparse_medoids
77 
78 f = open("mds.dat", "w")
79 print("# X, Y, cluster, is_medoid, N, E, x in Pt_{x}Au_{1-x}", file=f)
80 for i in range(0, len(db)):
81     db[i].info["clmds_coordinates"] = XY_sparse[i]
82     db[i].info["clmds_cluster"] = C_sparse[i]
83     db[i].info["clmds_medoid"] = i in M_sparse
84     print(*XY_sparse[i], C_sparse[i], i in M_sparse, len(db[i]), db[i].info["energy"], db[i].symbols.count("Pt")/len(db[i]), file=f)
85 
86 f.close()
87 write("db1.xyz", db)
88 ###############################################################################################

The code will select a series of "medoids" or representative NPs, together with the embedding in two dimensions of the data. Each point in the MDS map represents a NP, and distances on the plot represent how similar two NPs are: the closer they are on the plot the more similar they are in the significantly higher-dimensional configuration space (as goven by the kernel similarities). The initial database db0.xyz has been updated with information related to the clustering and embedding. You can download a sample updated file db1.xyz from here. In the "info" line, the tags "clmds_coordinates", "clmds_cluster" and "clmds_medoid" will appear, respectively indicating the 2D MDS embedding coordinates, cluster it belongs to and whether it's a medoid or not of the corresponding NP.

Now, let's make a plot_nps directory and run this to get the cartoons for the medoid NPs:

 1 import sys
 2 from ase.io import read,write
 3 from ase.visualize import view
 4 import numpy as np
 5 from ovito.io.ase import ase_to_ovito
 6 from ovito.pipeline import StaticSource, Pipeline
 7 from ovito.vis import Viewport, BondsVis, ParticlesVis, TachyonRenderer
 8 from ovito.io import import_file
 9 from ovito.modifiers import CreateBondsModifier, ColorCodingModifier
10 from scipy.special import erf
11 
12 db0 = read("../db1.xyz", index=":")
13 cl = []
14 db = []
15 
16 for atoms in db0:
17     if atoms.info["clmds_medoid"]:
18         db.append(atoms)
19         cl.append(atoms.info["clmds_cluster"])
20 
21 dbt = np.array(db, dtype=object)
22 db = dbt[cl]
23 
24 for k in range(0, len(db)):
25     atoms = db[k].copy()
26     try:
27         del atoms.arrays["fix_atoms"]
28     except:
29         pass
30 
31     atoms_data = ase_to_ovito(atoms)
32     pipeline = Pipeline(source = StaticSource(data = atoms_data))
33     pipeline.add_to_scene()
34 
35     n_Pt = atoms.symbols.count("Pt")
36     n_Au = atoms.symbols.count("Au")
37     n_H = atoms.symbols.count("H")
38 
39     types = pipeline.source.data.particles.particle_types_
40 
41     radius = {"Au": 1.8, "Pt": 1.8, "H": 0.5}
42     for n in range(1,4):
43         try:
44             el = types.type_by_id_(n).name
45             types.type_by_id_(n).radius = radius[el]
46         except:
47             pass
48 
49     colors = np.zeros([len(atoms),3])
50     for i in range(0, len(atoms)):
51         if atoms[i].symbol == "Pt":
52             colors[i] = np.array([0.8,0.8,0.8])
53         elif atoms[i].symbol == "Au":
54             colors[i] = np.array([1,1,0])
55         elif atoms[i].symbol == "H":
56             colors[i] = np.array([1,1,1])
57 
58     pipeline.source.data.particles_.create_property("Color", data=colors)
59 
60     tachyon = TachyonRenderer(shadows=False, direct_light_intensity=1.1)
61 
62     pipeline.source.data.cell_.vis.render_cell = False
63 
64     vp = Viewport()
65     vp.type = Viewport.Type.Perspective
66     direction = (2, 3, -1)
67     vp.camera_dir = direction
68     vp.camera_pos = atoms.get_center_of_mass() - direction / np.dot(direction,direction)**0.5 * 30.
69     vp.render_image(filename = "np_png/%i.png" % (k+1), size=(120,120), alpha=False, renderer=tachyon)
70     pipeline.remove_from_scene()
71 
72 #   Print progress
73     sys.stdout.write('\rProgress:%6.1f%%' % ((k + 1)*100./len(db)) )
74     sys.stdout.flush()

We can see how the most representative NPs span all alloy compositions encountered in the database. Here we chose 22 clusters/medoids for the k-medoids algorithm. In k-medoids this number is chosen by the user, althugh one can also sweep over different values and monitor the evolution of some "incoherence" measure, such as average intracluster distances, to select the optimal number of clusters.

Now, we can also plot the MDS maps to visualize the global dissimilarities at a glance:

 1 set term pngcairo size 1200,480
 2 
 3 set output "mds_np.png"
 4 
 5 set multiplot layout 1,3
 6 
 7 set size ratio -1
 8 set format x ""
 9 set format y ""
10 
11 unset xtics
12 unset ytics
13 
14 set key right box
15 
16 set title "PtAu NP according to cluster"
17 plot "../mds.dat" u 1:2:3 lc var pt 7 not, \
18      "" u (stringcolumn(4) eq "True" ? $1 : 1/0):2 pt 7 ps 3 lc "green" t "Medoids", \
19      "" u (stringcolumn(4) eq "True" ? $1 : 1/0):2:(sprintf("%i", $3+1)) w labels not
20 
21 set title "PtAu NP according to composition"
22 set cblabel "x in Pt_{x}Au_{1-x}"
23 plot "../mds.dat" u 1:2:7 palette pt 7 not, \
24      "" u (stringcolumn(4) eq "True" ? $1 : 1/0):2 pt 6 ps 1.4 lw 4 lc "green" t "Medoids"
25 
26 set title "PtAu NP according to energy"
27 set cblabel "Total energy (eV/atom)"
28 plot "../mds.dat" u 1:2:($6/$5) palette pt 7 not, \
29      "" u (stringcolumn(4) eq "True" ? $1 : 1/0):2 pt 6 ps 1.4 lw 4 lc "green" t "Medoids"

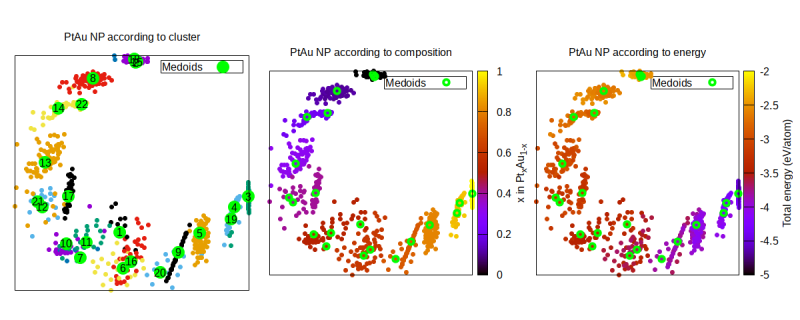
Here we are plotting the similarities on the XY coordinates and choose three different color codings to display further information: to which data cluster the NP corresponds to, what is the composition of each NP, and what is the energy (per atom) of each NP. Unsurprisingly, there is a very strong correlation between these three quantities, because for these NP the most differentiating property is their chemical composition (i.e., their Pt fraction).

Analyzing the individual atomic sites

After using the global SOAP kernel [math]\displaystyle{ K(I,J) }[/math] to compare and analyze the structure of whole NPs, we are going to use the regular (atom- or site-wise) SOAP kernel [math]\displaystyle{ k(i,j) }[/math] to gain insight into the site distribution in our database. We are further going to use some of the ase_tools functionality to identify the surface atoms. This might be relevant, e.g., for applications in catalysis. We now use the sparsification features of cl-MDS because the number of atomic sites is too large compared to the number of NPs, and this would significantly slow down the clustering+embedding procedure if we were using the entire set of data points. The following script takes care of all the different steps:

  1 import sys
  2 from quippy.descriptors import Descriptor
  3 from quippy.convert import ase_to_quip
  4 import numpy as np
  5 from ase.io import read,write
  6 import cluster_mds as clmds
  7 import kmedoids
  8 from ase_tools import surface_list
  9 
 10 # Read in the database
 11 db = read("db1.xyz", index=":")
 12 
 13 
 14 # Create mappings
 15 which_structure = []
 16 which_atom = []
 17 map_back = {}
 18 local_energy = []
 19 k = 0
 20 for i in range(0, len(db)):
 21     le = db[i].get_array("local_energy")
 22     for j in range(0, len(db[i])):
 23         which_structure.append(i)
 24         which_atom.append(j)
 25         map_back[i,j] = k
 26         local_energy.append(le[j])
 27         k += 1
 28 
 29 
 30 # Rolling sphere algorithm parameters
 31 r_min = 4.
 32 r_max = 4.5
 33 n_tries = 1000000
 34 
 35 
 36 # Build a list of surface atoms
 37 surf_list_all = []
 38 is_surface = np.full(len(which_atom), False, dtype=bool)
 39 k = 0
 40 for i in range(0, len(db)):
 41     surf_list = surface_list(db[i], r_min, r_max, n_tries, cluster=True)
 42     surf_list_all.append(surf_list)
 43     for j in range(0,len(db[i])):
 44         if j in surf_list:
 45             is_surface[k] = True
 46         k += 1
 47     if True:
 48         sys.stdout.write('\rBuilding list of surface atoms:%6.1f%%' % (float(i)*100./len(db)) )
 49         sys.stdout.flush()
 50 
 51 
 52 ###############################################################################################
 53 # This builds the kernel for the site-wise cl-MDS map
 54 n_cl = 22 # number of clusters
 55 cutoff = 5.7; dc = 0.5; sigma = 0.5
 56 zeta = 6
 57 soap = {"Au": 'soap_turbo alpha_max={8 8} l_max=8 rcut_soft=%.4f rcut_hard=%.4f \
 58                atom_sigma_r={%.4f %.4f} atom_sigma_t={%.4f %.4f} \
 59                atom_sigma_r_scaling={0. 0.} atom_sigma_t_scaling={0. 0.} \
 60                radial_enhancement=1 amplitude_scaling={1. 1.} \
 61                basis="poly3gauss" scaling_mode="polynomial" species_Z={78 79} \
 62                n_species=2 central_index=2 central_weight={1. 1.} \
 63                compress_mode=trivial' % (cutoff-dc, cutoff, *(4*[sigma])),
 64         "Pt": 'soap_turbo alpha_max={8 8} l_max=8 rcut_soft=%.4f rcut_hard=%.4f \
 65                atom_sigma_r={%.4f %.4f} atom_sigma_t={%.4f %.4f} \
 66                atom_sigma_r_scaling={0. 0.} atom_sigma_t_scaling={0. 0.} \
 67                radial_enhancement=1 amplitude_scaling={1. 1.} \
 68                basis="poly3gauss" scaling_mode="polynomial" species_Z={78 79} \
 69                n_species=2 central_index=1 central_weight={1. 1.} \
 70                compress_mode=trivial' % (cutoff-dc, cutoff, *(4*[sigma]))}
 71 
 72 d = {}
 73 
 74 d["Pt"] = Descriptor(soap["Pt"])
 75 d["Au"] = Descriptor(soap["Au"])
 76 
 77 qs = []
 78 for atoms in db:
 79     at = ase_to_quip(atoms)
 80     N = {}
 81     q = {}
 82     for i in range(0,len(atoms)):
 83         symb = atoms.symbols[i]
 84         if symb not in N:
 85             N[symb] = 0
 86             q[symb] = d[symb].calc_descriptor(at)
 87         this_q = q[symb][N[symb]]
 88         qs.append(this_q)
 89         N[symb] += 1
 90 
 91 dist = np.zeros([len(qs),len(qs)])
 92 n = 0
 93 for i in range(0,len(qs)):
 94     arg = 1. - np.dot(qs[:], qs[i])**zeta
 95     arg2 = np.clip(arg, 0, 1)
 96     dist[i,:] = np.sqrt(arg2)
 97     sys.stdout.write('\rBuilding distance matrix:%6.1f%%' % (float(i)*100./len(qs)) )
 98     sys.stdout.flush()
 99 
100 print("    MBytes: ", dist.nbytes/1024/1024)
101 print("")
102 
103 # Embedding
104 M, C = kmedoids.kMedoids(dist, n_cl, n_iso=n_cl//2, init_Ms="isolated", n_inits=10)
105 data = clmds.clMDS(dist_matrix = dist, sparsify="cur", n_sparse=500)
106 data.cluster_MDS([n_cl,1], weight_cluster_mds=2., weight_anchor_mds=10., init_medoids=M)
107 list_sparse = data.sparse_list
108 XY_sparse = data.sparse_coordinates
109 C_sparse = data.sparse_cluster_indices
110 M_sparse = data.sparse_medoids
111 M = []
112 for k in M_sparse:
113     M.append(list_sparse[k])
114 
115 M = np.array( M, dtype=int )
116 indices = np.array( list(range(0,len(dist))), dtype=int )
117 data.compute_pts_estim_coordinates( indices=indices )
118 XY = data.estim_coordinates
119 C = data.estim_cluster_indices
120 # Transform to usual cluster array
121 C_usual = []
122 for i in range(0, n_cl):
123     C_usual.append([])
124 
125 for i in range(0, len(C)):
126     C_usual[C[i]].append(i)
127 
128 C_list = C
129 C = C_usual
130 #
131 
132 k = 0
133 for atoms in db:
134     atoms.set_array("clmds_cluster", C_list[k:k+len(atoms)])
135     atoms.set_array("clmds_coordinates", XY[k:k+len(atoms)])
136     k += len(atoms)
137 
138 k = 0
139 for atoms in db:
140     is_medoid = np.full(len(atoms), False)
141     is_surface2 = np.full(len(atoms), False)
142     for i in range(0, len(atoms)):
143         if is_surface[k]:
144             is_surface2[i] = True
145         if k in M:
146             is_medoid[i] = True
147         k += 1
148     atoms.set_array("clmds_medoid", is_medoid)
149     atoms.set_array("surface", is_surface2)
150 
151 
152 f = open("mds_sites.dat", "w")
153 print("# X, Y, cluster, is_medoid, is_surface, le, species, N of NP", file=f)
154 k = 0
155 for i in range(0, len(db)):
156     for j in range(0, len(db[i])):
157         print(*XY[k], C_list[k], k in M, is_surface[k], local_energy[k], db[i].symbols[j], len(db[i]), file=f)
158         k += 1
159 
160 f.close()
161 
162 
163 
164 write("db2.xyz", db)
165 ###############################################################################################

We have again updated the database, this time with per-atom information. The new db2.xyz file (an example of which you can download here) now contains extra columns with the cluster and embedding information for all atoms, as well as a column indicating whether the atom is a surface atom or not. Let us now create a new directory, plot_sites, to run the plotting script within, again aiming to keep our top directory as clean as possible.

Note how our Ovito code is now significantly more complex, since we are doing two things: 1) we are aligning the line of view with the center of mass of the NP and the position of the medoids; 2) when the medoid is not a surface atom, we are adding transparency to all the atoms between the medoid and the viewer. Besides, we are doing the less sophisticated operation of mixing the color of the Pt/Au atom (gray/yellow, respectively) with red, to highlight the medoid.

  1 import sys
  2 from ase.io import read,write
  3 from ase.visualize import view
  4 import numpy as np
  5 from ovito.io.ase import ase_to_ovito
  6 from ovito.pipeline import StaticSource, Pipeline
  7 from ovito.vis import Viewport, BondsVis, ParticlesVis, TachyonRenderer
  8 from ovito.io import import_file
  9 from ovito.modifiers import CreateBondsModifier, ColorCodingModifier
 10 from scipy.special import erf
 11 
 12 db0 = read("../db2.xyz", index=":")
 13 
 14 db = []
 15 cluster = []
 16 for k in range(0, len(db0)):
 17     atoms = db0[k]
 18     medoid = atoms.get_array("clmds_medoid")
 19     del atoms.arrays["clmds_medoid"]
 20     for i in range(0, len(atoms)):
 21         if medoid[i]:
 22             this_medoid = np.full(len(atoms), False)
 23             this_medoid[i] = True
 24             atoms2 = atoms.copy()
 25             atoms2.set_array("clmds_medoid", this_medoid)
 26             db.append(atoms2)
 27             cluster.append(atoms2.arrays["clmds_cluster"][i])
 28 
 29 for k in range(0, len(db)):
 30     atoms = db[k].copy()
 31     medoid = atoms.get_array("clmds_medoid")
 32     surface = atoms.get_array("surface")
 33     slice = False
 34     transparency = np.zeros(len(atoms))
 35     cm = atoms.get_center_of_mass()
 36     atoms.positions -= cm
 37     for i in range(0, len(atoms)):
 38         if medoid[i] and not surface[i]:
 39             v = atoms[i].position
 40             for j in range(0, len(atoms)):
 41                 u = atoms[j].position
 42                 if np.dot(v,u) > np.dot(v,v) and j != i:
 43                     transparency[j] = 0.9
 44             direction = atoms.positions[i]
 45             dist = 30.
 46         elif medoid[i]:
 47             direction = atoms.positions[i]
 48             dist = 25.
 49 
 50     try:
 51         del atoms.arrays["fix_atoms"]
 52     except:
 53         pass
 54     try:
 55         del atoms.arrays["clmds_medoid"]
 56     except:
 57         pass
 58     try:
 59         del atoms.arrays["medoid"]
 60     except:
 61         pass
 62     try:
 63         del atoms.arrays["surface"]
 64     except:
 65         pass
 66     try:
 67         del atoms.arrays["clmds_cluster"]
 68     except:
 69         pass
 70 
 71     atoms_data = ase_to_ovito(atoms)
 72     pipeline = Pipeline(source = StaticSource(data = atoms_data))
 73     pipeline.add_to_scene()
 74 
 75     n_Pt = atoms.symbols.count("Pt")
 76     n_Au = atoms.symbols.count("Au")
 77     n_H = atoms.symbols.count("H")
 78 
 79     types = pipeline.source.data.particles.particle_types_
 80 
 81     radius = {"Au": 1.8, "Pt": 1.8, "H": 0.5}
 82     for n in range(1,4):
 83         try:
 84             el = types.type_by_id_(n).name
 85             types.type_by_id_(n).radius = radius[el]
 86         except:
 87             pass
 88 
 89     colors = np.zeros([len(atoms),3])
 90     for i in range(0, len(atoms)):
 91         if medoid[i]:
 92             k1 = 0.7; k2 = 0.3
 93         else:
 94             k1 = 1.; k2 = 0.
 95         if atoms[i].symbol == "Pt":
 96             colors[i] = k1*np.array([0.8,0.8,0.8]) + k2*np.array([1,0,0])
 97         elif atoms[i].symbol == "Au":
 98             colors[i] = k1*np.array([1,1,0]) + k2*np.array([1,0,0])
 99         elif atoms[i].symbol == "H":
100             colors[i] = k1*np.array([1,1,1]) + k2*np.array([1,0,0])
101 
102     pipeline.source.data.particles_.create_property("Color", data=colors)
103     pipeline.source.data.particles_.create_property("Transparency", data=transparency)
104 
105     tachyon = TachyonRenderer(shadows=False, direct_light_intensity=1.1)
106 
107     pipeline.source.data.cell_.vis.render_cell = False
108 
109     vp = Viewport()
110     vp.type = Viewport.Type.Perspective
111 
112     vp.camera_dir = -direction
113     vp.camera_pos = atoms.get_center_of_mass() + direction + direction / np.dot(direction,direction)**0.5 * dist
114     vp.render_image(filename = "sites_png/%i.png" % (cluster[k]+1), size=(120,120), alpha=False, renderer=tachyon)
115     pipeline.remove_from_scene()

This is what the Ovito rendering of the medoid sites looks like:

Finally, let's plot the MDS maps and color code according to useful information:

 1 set term pngcairo size 1200,480
 2 
 3 set output "mds_sites.png"
 4 
 5 set multiplot layout 1,3
 6 
 7 set size ratio -1
 8 set format x ""
 9 set format y ""
10 
11 unset xtics
12 unset ytics
13 
14 set key right box opaque
15 
16 set title "Atomic sites according to cluster"
17 plot "../mds_sites.dat" u 1:2:3 lc var pt 7 not, \
18      "" u (stringcolumn(4) eq "True" ? $1 : 1/0):2 pt 7 ps 3 lc "green" t "Medoids", \
19      "" u (stringcolumn(4) eq "True" ? $1 : 1/0):2:(sprintf("%i", $3+1)) w labels not
20 
21 set title "Sites according to composition and surface/bulk"
22 plot "../mds_sites.dat" u 1:(stringcolumn(7) eq "Pt" && stringcolumn(5) eq "True" ? $2 : 1/0) pt 7 t "Pt (surface)", \
23      "../mds_sites.dat" u 1:(stringcolumn(7) eq "Pt" && stringcolumn(5) eq "False" ? $2 : 1/0) pt 7 t "Pt (bulk)", \
24      "../mds_sites.dat" u 1:(stringcolumn(7) eq "Au" && stringcolumn(5) eq "True" ? $2 : 1/0) pt 7 t "Au (surface)", \
25      "../mds_sites.dat" u 1:(stringcolumn(7) eq "Au" && stringcolumn(5) eq "False" ? $2 : 1/0) pt 7 t "Au (bulk)", \
26      "" u (stringcolumn(4) eq "True" ? $1 : 1/0):2 pt 6 ps 1.4 lw 4 lc "green" t "Medoids"
27 
28 set title "Local site energy"
29 set cblabel "Local GAP energy (eV/atom)"
30 plot "../mds_sites.dat" u 1:2:6 palette pt 7 not, \
31      "" u (stringcolumn(4) eq "True" ? $1 : 1/0):2 pt 6 ps 1.4 lw 4 lc "green" t "Medoids"

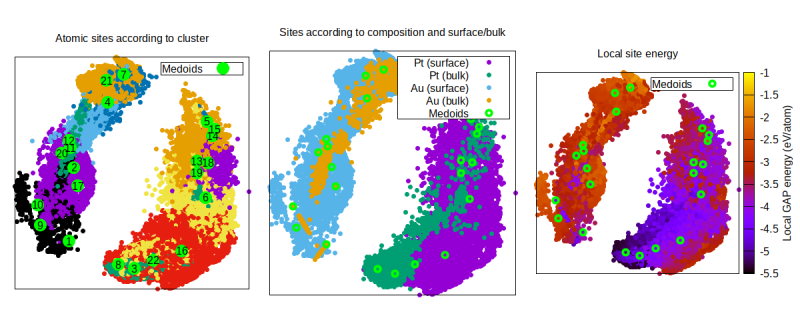
We have now chosen to color code that data points (of which we have many more than before!) by cluster, species+bulk/surface character, and local GAP energy. We can see that the clustering and embedding algorithms separate preferentially according to species, but also by surface/bulk character. It is also interesting to see how the GAP local energy clearly establishes bulk Pt atoms to be more stable than surface Pt atoms. However, take this with a grain of salt: due to the very small size of these NPs, there is no proper bulk. Nevertheless, the stabilizing effect of the increased atomic coordination is quite evident going from the interior sites to the surface sites.